8. New Experiments: Sum of Squares and Plotting III¶

Exploring Questions
Congruences
- Exploration 10
  - More Plotting and Graphics in Two Dimensions

What possible Python buitin data structure(s) do you think will be best in storing the numbers that can be written?

my_list_database = [0, 1, 2, 4, 5]

What if, in addition to the possible positive integers that can we can write as the sum of two squares, we also want to know the number of ways that they can be written. What Python builtin data structure(s) do you think will be suitable in this case?

Let us create a database of some of the numbers that can be written starting with those that we tried with pens and paper.

number_of_ways = [1, 2, 1, 2, 2]

possible_database = list(zip(my_list_database, number_of_ways)); possible_database

A more effective way is to use Python’s dictionary data structure. If that is the case, then we could also have passed the Python variable possible_database to Python’s dict function create dictionary object. That is,

dict(possible_database)

Or we could also start everything with a dictionary and type in the data we want to collect.

sum_of_square_database = {0: [(0,0)], 1: [(1,0), (0,1)], 2:[(1,1)]}; sum_of_square_database

We can update the dictionary object assigned to the Python variable sum_of_square_database as follows:

sum_of_square_database[4] = [(0,2), (2, 0)]

sum_of_square_database

sum_of_square_database[5] = [(1,2), (2, 1)]

sum_of_square_database

After a while you will want to think of an effective way of doing this by using some Python programming construct? What could be your possible effective solution?

sum_of_square_database = {}
for a in range(20):
    for b in range(20):
        m = a^2 + b^2

Hopefully, by now you should have a fair amount of data in sum_of_square_database. Let us now begin exploring the questions we posed regarding the sum of two squares by querying the database we have created. Here are the list of questions we posed:

Which positive integers can be written as a sum of two squares?
Which ones cannot?
Which positive integers can be written as a sum of squares of it factors?
Can there be a formula for expressing $n$ as the sum of two positive square numbers?
Which numbers can be written as a sum of squares of 2 prime numbers?
These numbers that can be written as a sum of two squares, are they odd or even?
Given $a$ and $b$ are prime, is the sum of their squares, $a^{2}+b^{2}$ prime?
Can the square roots of numbers be written in any other form aside from $x^{2} + 0^{2}$ ?
Is there more than one way to get the $n$ , and if they is, what’s the relationship between the $a$ , $b$ and $n$ .

I also possed the following:

Are there any special types of numbers that can be written? (Or that cannot?)
- Primes
- even/odd, modulo 3, modulo 4, modulo 5, etc..
- A combination of the above

Let us take a look at a possible way in exploring the first three questions we possed in class last time.

8.1. Exploring Questions ¶

The goal of this subsection is answer the first three questions that we possed concerning the sum of squares problems. You will learn what it means to query the database we have created. Let us begin with the first question.

8.1.1. Exploration 1 ¶

The question to explore is:

Which positive integers can be written as a sum of two integer squares?

What will be a possible answer to this?

sum_of_square_database

That seems to answer the question. However, I think there is more we can ask here. For example, Is there more to explore about these numbers? Is there anything common with them or a subset of them? What do you think we can do?

We may come back to this later.

8.1.2. Exploration 2 ¶

The question to explore is:

Which positive numbers cannot be written as a sum of two integer squares?

What will be a possible answer to this? How would you encode this in Python in order to query the database sum_of_square_database?

Is there more to explore about these numbers? Is there anything common with them or a subset of them? What do you think we can do?

We may come back to this later.

8.1.3. Exploration 3 ¶

The question to explore is:

Which positive integers can be written as a sum of two integer squares of it factors?

In other words, among those positive integers $n$ can be written as $n = a^{2} + b^{2}$ with $a$ and $b$ as integers, which them are factors of $n$ . That is, $a$ and $b$ both divides $n$ .

What will be a possible answer to this? How would you encode this in Python in order to query the database sum_of_square_database?

8.1.4. Exploration 4 ¶

The question to explore is:

Can there be a formula for expressing :math:`n` as the sum of two positive square numbers?

You may want to skip this for now.

8.1.5. Exploration 5 ¶

The question to explore is:

These numbers that can be written as a sum of two squares, are they odd or even?

8.1.6. Exploration 6 ¶

The question to explore is:

Given :math:`a` and :math:`b` are prime, is the sum of their squares, :math:`a^{2}+b^{2}` prime?

Hint: You may want to use the SageMath function ``is_prime``. Try and read the documentation so you know how to use it.

8.1.7. Exploration 7 ¶

The question to explore is:

Can the square roots of numbers be written in any other form aside from :math:`x^{2} + 0^{2}`?

In other words, if $n$ is a square, i.e., $\exists\, x\in\mathbb{Z}$ with $n = x^{2}$ , then are there positive integers $a, b$ such that $n = a^{2} + b^{2}$ ?

8.1.8. Exploration 8 ¶

The question to explore is:

Is there more than one way to write a positive integer :math:`n` as the sum of two integer squares :math:`a^{2} + b^{2}`, and if they is, what’s the relationship between :math:`n`, :math:`a` and :math:`b`?

8.1.9. Exploration 9 ¶

The question to explore is:

Can prime numbers be written as a sum of two squares and if so, do they follow some underlying pattern?

8.2. Congruences ¶

I want to introduce an elementary operation that might be useful in our exploration; namely, modulo arithmetic. You should have seen this before. It has something to do with divisibilty.

To start, let’s compute. What is the remainder of $25$ when divided by $6$ ? Do it by hand first.

mod(25, 6)

From the division algorithm, we know that such a remainder is unique. If we divide $x$ by $m$ , then $0\leq {\rm mod}(x,m)< m$ . But lots and lots of different numbers can have the same remainder!

[mod(num, 6) for num in [1, 7, 13, 19, 25, -5, -11, 6001, -17]]

In mathematics, what we often do in such a situation where structure is shared is to connect things with a relation.

A relation is a very general notion, and basically it exists once you define it. Our relation will be called congruence, denoted by $\equiv$ and it is massively important. We essentially use the same definitions and notation that Gauss came up with.

Definition: We say that $a$ is congruent to $b$ modulo $n$ , or $a \equiv b \, ({\rm mod} \, n)$ , precisely if

System Message: WARNING/2 (n\mid (a−b))

latex exited with error [stdout] This is pdfTeX, Version 3.14159265-2.6-1.40.19 (TeX Live 2019/dev/Debian) (preloaded format=latex) restricted \write18 enabled. entering extended mode (./math.tex LaTeX2e <2018-12-01> (/usr/share/texlive/texmf-dist/tex/latex/base/article.cls Document Class: article 2018/09/03 v1.4i Standard LaTeX document class (/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo)) (/usr/share/texlive/texmf-dist/tex/latex/base/inputenc.sty) (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty For additional information on amsmath, use the `?' option. (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty)) (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty) (/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty)) (/usr/share/texlive/texmf-dist/tex/latex/amscls/amsthm.sty) (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)) (/usr/share/texlive/texmf-dist/tex/latex/anyfontsize/anyfontsize.sty) (/usr/share/texlive/texmf-dist/tex/latex/tools/bm.sty) (./math.aux) (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd) (/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd) ! Package inputenc Error: Unicode character − (U+2212) (inputenc) not set up for use with LaTeX. See the inputenc package documentation for explanation. Type H <return> for immediate help. ... l.13 \fontsize{13}{16}\selectfont $n\mid (a− b)$ [1] (./math.aux) ) (see the transcript file for additional information) Output written on math.dvi (1 page, 304 bytes). Transcript written on math.log.

.

This is exactly the same thing as leaving the same remainder.  It is
very useful to try to prove that these conditions are the same.
In our case, saying  (mod ) is the
same as saying  and  and
.
This idea gives us a lot of power.  For instance, calculating
 (mod 3) instantaneous for me - it’s .

I can check it with SageMath:

%time mod(2^1000000000,3)

Yet I did it instantaneously in my head. Of course, the reason is not that I am clever, but that congruence can be turned into arithmetic! Here are two useful properties:

If $a\equiv b$ (mod $m$ ), then $a+c\equiv b+c$ (mod $m$ ).
If $a\equiv b$ (mod $m$ ), then $ac\equiv bc$ (mod $m$ ).

Now I reveal my secret: $2\equiv -1$ (mod 3), and $(-1)^{1000000000}=1$ , like all even powers of negative one. Ta-dah!

What I’ve done is first think of the original number as in the congruence, and then taken its power. SageMath verifies this approach is much faster, and even for much bigger powers:

b = mod(2,3); b

print(type(b))

%time b^1000000000000000000000000000000

What was computed above is not a trick; I definitely couldn’t do $2000^{1000}$ , or even $16^{1000}$ , in my head.

There is another set of properties that congruence has. Congruence is reflexive, symmetric, and transitive. That is, all the things you know are true about equality are also true about congruence (with a particular modulus $n$ picked, of course).

For any $a\in \mathbb{Z}$ , $a\equiv a$ (mod $n$ ).
If $a\equiv b$ mod ( $n$ ), then $b\equiv a$ (mod $n$ ).
If it happens that both $a\equiv b$ and $b\equiv c$ (mod $n$ ), then $a\equiv c$ (mod $n$ ) as well.

If we combine all of these facts, it basically means we can divide up all the integers into “equivalence classes”. That is, $\mathbb{Z}$ can be broken up into disjoint pieces which we are free to consider as units, and which stay different.

We denote such a class by the notation

$[a]=\{\text{all numbers congruent to }a\text{ modulo }n\}\; .$

So, for instance, the equivalence class we started with is

$[1]=\{1, 7, 13, 19, 25, -5, -11, 6001,\ldots\}$

or perhaps better written as

$\{1+6n\mid n\in\mathbb{Z}\}=[1]\; .$

Definition: We call the set of equivalence classes modulo $n$ the integers modulo n, and denote them by $\mathbb{Z}_n$ .

%time mod(2^3000000000,7)

%time mod(2,7)^3000000000

I knew this one too. Figure out why with your group members.

Then spend a while making up more examples of this.
Or, try to figure out how I know that $123456$ is divisible by $3$ but not divisible by $9$ , using congruences.

Now let us use the concept of modulo arithmetic in our exploration. In your groups, try to come up with more questions which uses the modulo operation and explore together. Try and record your findings.

Before you query the database sum_of_square_database with the questions you have possed as a group, take a look at Exploration 10, where I possed a question that makes use of the modulo operation. Explore this a group and record your findings. Afterwards, you should explore the questions that you came up with. Again remember to record your findings.

8.2.1. Exploration 10 ¶

The question to explore is:

Can even/odd numbers modulo 3, modulo 4, modulo 5, etc., be written as a sum of two squares and if so, do they follow some underlying pattern?

Can you think of a way to solve this problem? Hint: What do you know about equations of this form :math:`n = a^{2} + b ^{2}`?

var('y')
n = 5
P = implicit_plot( x^2 + y^2 == n, (x, -sqrt(n), sqrt(n)), (y, -sqrt(n), sqrt(n)) )
lattice_pts = [ [i,j] for i in [floor(-sqrt(n))..ceil(sqrt(n))] for j in [floor(-sqrt(n))..ceil(sqrt(n))] ]
plot_lattice_pts = points(lattice_pts, rgbcolor = (0, 0, 0), pointsize = 10)
P + plot_lattice_pts

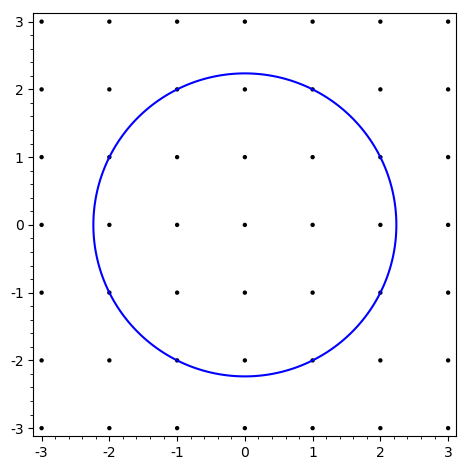
This brings up the question of how to do such plotting in the first place? We will look at this in more detail in the next Section.

8.2.1.1. More Plotting and Graphics in Two Dimensions ¶

There is absolutely no way we could cover all the graphics in SageMath (or the program that does it for SageMath, matplotlib) in one day, or even a week. We will look at a bunch of different resources you have access to, and see lots of different plot types. As we go through these resources, think of how they will be of in solving our new experiment or where you could have used them some time back in your academic career. I definitely do not know everything about the plotting command. Nevertheless, you may interrupt me with your question so that we can explore the solution together.

We will begin with the advanced 2D-plotting in the built-in live documentation. (This link only works if you are already using SageMath; the non-live version is here.
There are two very important pages with many, MANY examples - the documentation for plot and that for showing graphics.
The general plotting reference - there are a lot of surprises, like animation, etc.

Remember, you should feel free to stop listening for a while if you can want to try something out!

Once we’ve seen enough examples, please either start using SageMath to explore the sums of squares, or try to recreate your favorite graphic using SageMath!

8. New Experiments: Sum of Squares and Plotting III¶

8.1. Exploring Questions ¶

8.1.1. Exploration 1 ¶

8.1.2. Exploration 2 ¶

8.1.3. Exploration 3 ¶

8.1.4. Exploration 4 ¶

8.1.5. Exploration 5 ¶

8.1.6. Exploration 6 ¶

8.1.7. Exploration 7 ¶

8.1.8. Exploration 8 ¶

8.1.9. Exploration 9 ¶

8.2. Congruences ¶

8.2.1. Exploration 10 ¶

8.2.1.1. More Plotting and Graphics in Two Dimensions ¶

Table of Contents

This Page